人口老龄化、人力资本结构与科技创新

蒋长流; 司怀涛

doi:10.19979/j.cnki.issn10082689.2022030128

人口老龄化、人力资本结构与科技创新—基于空间杜宾与中介效应模型的实证研究

doi: 10.19979/j.cnki.issn10082689.2022030128

安徽大学经济学院合肥 230601

基金项目: 国家社科基金项目“新型城镇化进程中低碳发展转型的激励和约束机制研究”（编号：14BJL104）；安徽省科技创新战略与软科学研究重大专项“全社会R&D投入持续稳定提高的政策措施与途径研究（编号：1706a02020046）”

详细信息

作者简介:
蒋长流（1967—），男，安徽合肥人，安徽大学经济学院教授

司怀涛（1991—），男，山东菏泽人，安徽大学经济学院硕士

中图分类号: F204
计量
- 文章访问数: 532
- HTML全文浏览量: 167
- PDF下载量: 45
- 被引次数: 0
出版历程
- 收稿日期: 2022-03-30
- 网络出版日期: 2022-10-10
- 刊出日期: 2022-10-25

Population Aging, Human Capital Structure and Innovation in Science and TechnologyAn Empirical Study Based on Spatial Durbin Model and Mediation Effect

School of Economics, Anhui University, Hefei 230601, China

摘要

摘要: 科技创新是推动经济高质量发展的核心因素，而人口老龄化与人力资本结构对科技创新具有重要影响。文章采用2008—2017年31个省面板数据，基于空间杜宾模型，对人口老龄化、人力资本结构与科技创新之间的关系进行了实证研究。空间杜宾模型的实证结果显示，人口老龄化对本地区及邻近地区科技创新均具有显著的抑制作用，而人力资本则可以显著促进本地区科技创新，但对于邻近地区，以不同数据指标测度的人力资本并未表现出预期的空间正向溢出。另外，人力资本中介效应检验结果显示，人力资本在人口老龄化影响科技创新的过程中存在部分遮掩效应。因而在人口老龄化程度不断加深的背景下，应不断优化人力资本结构，进一步增加科研投入，以促进区域创新能力的提升。
- 人口老龄化 /
- 人力资本结构 /
- 科技创新 /
- 空间杜宾模型 /
- 中介效应
Abstract: Scientific and technological innovation is the core factor to promote high-quality economic development, and population aging and human capital structure have an important impact on scientific and technological innovation. Using the panel data of 31 provinces from 2008 to 2017, based on the Spatial Durbin Model, this paper conducts an empirical study on the relations among population aging, human capital structure and scientific and technological innovation. The empirical results of the Spatial Durbin Model show that population aging has a significant inhibitory effect on scientific and technological innovation in the given region and its adjacent regions, while human capital can significantly promote scientific and technological innovation in the region. However, for adjacent regions, human capital measured by different data indicators does not show the expected spatial positive spillover. In addition, the mediation effect test results of human capital show that human capital has a partial masking effect in the process that population aging affects scientific and technological innovation. Therefore, in the context of the increasingly aging population, we should constantly optimize the human capital structure and further increase investments in research and development to facilitate the improvement of regional innovation capacity.
- population ageing /
- human capital structure /
- scientific and technological innovation /
- Spatial Durbin Model /
- Mediation Effect

HTML全文

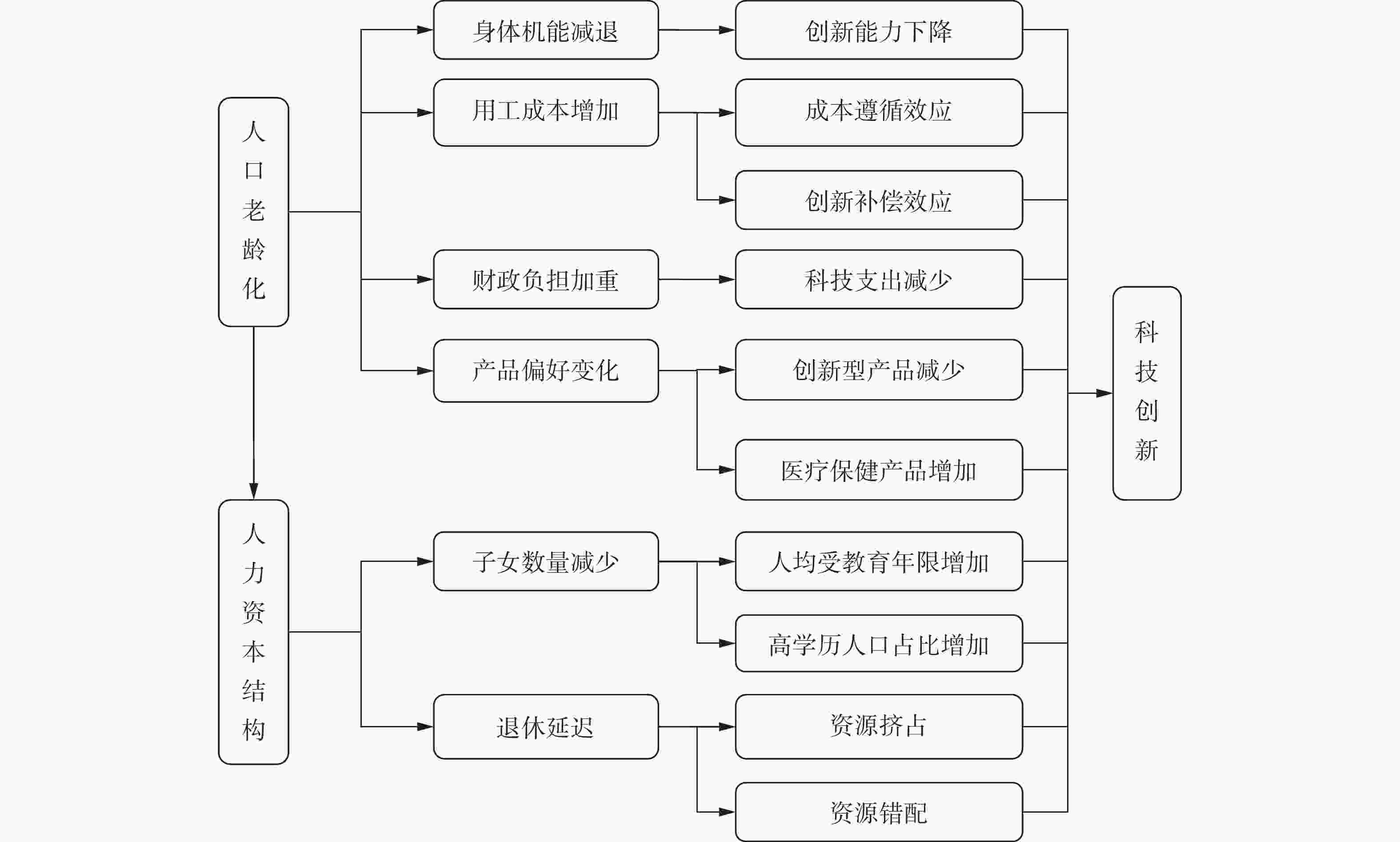
图 1 人口老龄化、人力资本结构影响科技创新的作用机理

下载: 全尺寸图片幻灯片

表 1 变量的描述性统计

符号	均值	标准差	最大值	最小值
TI	3.4969	5.5144	33.2652	0.0093
AGE	0.09550	0.01989	0.1428	0.04824
SCH	8.7712	1.1692	12.6651	4.2219
UNI	0.1165	0.0690	0.4761	0.0168
MAT	32.4535	51.4440	392.8942	1.6053
DOC	5.2848	13.2027	100.4591	0.00685
INCOME	0.4914	0.1943	1.317	0.2060
STR	1.1786	0.6460	4.8940	0.5271
INTE	1.2791	1.2638	6.5317	0.0115

下载: 导出CSV

表 2 科技创新的Moran’s I指数

年份	Moran’s I	P	年份	Moran’s I	P
2008	0.154^**	0.032	2013	0.248^***	0.002
2009	0.208^***	0.009	2014	0.235^***	0.004
2010	0.220^***	0.006	2015	0.232^***	0.005
2011	0.259^***	0.001	2016	0.225^***	0.006
2012	0.258^***	0.001	2017	0.176^**	0.016
注：、、**分别表示在10%、5%、1%水平下显著，下同。

下载: 导出CSV

表 3 空间面板模型选择的相关检验结果

检验方式	统计值	P值	检验方式	统计值	P值
LM-spatial lag	33.668^***	0.000	LR-spatial lag	8.04^**	0.0179
Robust LM-spatial lag	0.038	0.846	LR-spatial error	44.51^***	0.0000
LM-spatial error	98.481^***	0.000	Wald-spatial lag	17.97^***	0.0030
Robust LM-spatial error	64.851^***	0.000	Wald-spatial error	9.37^*	0.0950

下载: 导出CSV

表 4 空间回归结果

变量	模型一	模型二	模型三	模型四
AGE	−35.04352^^ （−2.55）	−35.2361^^^* (−2.65)	−34.61909^^ （−2.52）	−35.89913^^^* (−2.66)
SCH	0.9205213^* （1.88）
UNI		18.70748^^^* (3.18)
MAT			0.0269524^^^* （2.66）
DOC				0.1323956^^^* (3.03)
INCOME	10.42954^^^* （4.99）	8.822185^^^* （4.23）	6.905558^^^* （2.80）	6.295288^^ （2.53）
INTE	2.772078^^^* （16.44）	2.740461^^^* （16.78）	2.749099^^^* （16.33）	2.742093^^^* （16.13）
STR	0.8026596 （1.22）	0.9355746 (1.32)	−0.0341321 （−0.04）	−0.4596884 (−0.50)
WY	−0.6793776^^^* （−2.86）	−0.5948318^^^* （−2.61）	−0.7225381^^^* （−3.13）	−0.7186981^^^* （−3.12）
WAGE	−523.5879^^^* （−6.86）	−475.0227^^^* (−6.46)	−519.0659^^^* （−6.98）	−513.8045^^^* (−6.95)
WSCH	−0.8374223 （−0.21）
WUNI		−139.4957^^^* (−3.36)
WMAT			−0.0827274 （−1.20）
WDOC				−0.087933 (−0.33)
WINCOME	8.985366 （0.47）	17.36763 (0.92)	33.3751 （1.57）	29.70698 (1.40)
WINTE	6.104797^^^* （4.68）	5.709468^^^* （4.63）	6.086035^^^* （4.83）	6.46811^^^* （5.15）
WSTR	17.20265^^^* （3.54）	23.49289^^^* （4.05）	18.47324^^ （2.20）	12.31227 （1.55）

下载: 导出CSV

表 5 SDM模型的直接效应与间接效应回归结果

变量	模型一			模型二
变量	直接效应	间接效应	总效应	直接效应	间接效应	总效应
AGE	−22.43346 （−1.63）	−312.343^^^* （−4.99）	−334.776^^^* （−5.57）	−24.7902^* （−1.86）	−294.150^^^* （−4.85）	−318.94^^^* （−5.46）
SCH	1.005597^^ （2.16）	−1.029312 （−0.42）	−0.0237156 （−0.01）
UNI				21.79114^^^* （3.82）	−99.5894^^^* （−3.13）	−77.7983^^ （−2.41）
INCOME	10.31212^^^* （5.06）	1.457645 (0.11)	11.76976 （0.92）	8.813326^^^* （4.28）	7.918464 (0.63)	16.73179 （1.34）
INTE	2.666327^^^* （16.44）	2.649627^^^* （4.30）	5.315954^^^* （8.50）	2.649309^^^* （16.59）	2.676368^^^* （4.43）	5.325678^^^* （8.68）
STR	0.3748212 （0.60）	10.59769^^^* （3.19）	10.97251^^^* （3.25）	0.4161953 （0.65）	15.14662^^^* （3.52）	15.56282^^^* （3.48）

下载: 导出CSV

表 6 SDM模型的直接效应与间接效应回归结果

变量	模型三			模型四
变量	直接效应	间接效应	总效应	直接效应	间接效应	总效应
AGE	−21.53585^^ （−1.57）	−301.268^^^* （−5.04）	−322.804^^^* （−5.62）	−23.0405^^ （−1.70）	−297.960^^^* （−5.00）	−321.00^^^* （−5.64）
MAT	0.030730^^^* （3.12）	−0.0632968 （−1.57）	−0.0325673 （−0.80）
DOC				0.142004^^^* （3.46）	−0.10846^^^* （−0.72）	0.0335462 （0.21）
INCOME	6.075842^^ （2.42）	18.02925 (1.29)	24.10509^* （1.80）	5.551843^^ (2.21)	15.91258^^ (1.16)	21.46443 （1.62）
INTE	2.643069^^^* （16.27）	2.508298^^^* （4.24）	5.151367^^^* （8.54）	2.626735^^^* （15.97）	2.766952^^^* （4.57）	5.393687^^^* （8.69）
STR	−0.5944316 （−0.80）	11.33324^^ （2.26）	10.73881^^^* （2.02）	−0.87004 （−1.17）	7.629612^* （1.65）	6.75957 （1.37）

下载: 导出CSV

表 7 中介效应模型检验结果

变量	模型一			模型二
变量	模型1	模型2	模型3	模型1	模型2	模型3
AGE	−48.85932^^^* （−3.69）	1.003476 （0.44）	−50.6241^^^* （−3.93）	−48.85932^^^* （−3.69）	0.539541^^ （2.41）	−57.10399^^^* （−4.40）
SCH			1.59328^^^* （4.12）
UNI						15.46149^^^* （4.32）
控制变量	YES	YES	YES	YES	YES	YES
时间效应	YES	YES	YES	YES	YES	YES
地区效应	YES	YES	YES	YES	YES	YES
Cons	9.5133^^^* (4.05)	6.597448^^^* （22.62）	2.381202 （0.83）	9.5133^^^* (4.05)	−0.0378975 （−1.32）	11.82418^^^* （5.05）
R²	0.5888	0.4986	0.6128	0.5888	0.3603	0.6150

下载: 导出CSV

表 8 中介效应模型检验结果

变量	模型三			模型四
变量	模型1	模型2	模型3	模型1	模型2	模型3
AGE	−48.85932^^^* （−3.69）	562.547^^ （4.88）	−63.26615^^^* （−4.70）	−48.85932^^^* （−3.69）	88.9788^^ （3.52）	−60.90698^^^* （−4.66）
MAT			0.0259319^^^* （3.81）
DOC						0.1375569^^^* （4.49）
控制变量	YES	YES	YES	YES	YES	YES
时间效应	YES	YES	YES	YES	YES	YES
地区效应	YES	YES	YES	YES	YES	YES
Cons	9.5133^^^* (4.05)	−38.92285^^^* （−2.63）	10.89155^^^* （4.69）	9.5133^^^* (4.05)	−1.949625（−0.60）	9.445487^^^* （4.16）
R²	0.5888	0.3006	0.6095	0.5888	0.1306	0.6169

下载: 导出CSV

参考文献(25)

[1]	孙倩倩. 人口老龄化对技术创新的时空异质性效应研究[J]. 财经理论与实践,2021,42(3):118-123. doi: 10.16339/j.cnkihdxbcjb.2021.03.016
[2]	邵汉华,汪元盛. 人口结构与技术创新[J]. 科学学研究,2019,37(4):739-749. doi: 10.16192/j.cnki.1003-2053.2019.04.018
[3]	金昊,赵青霞. 人口结构转变如何影响技术创新−基于省级面板数据的实证分析[J]. 宏观经济研究,2019(12):130-147. doi: 10.16304/j.cnki.11-3952/f.2019.12.013
[4]	杨校美. 人口老龄化会影响技术创新吗?−来自G20的经验证据[J]. 华东经济管理,2018,32(6):115-123. doi: 10.19629/j.cnki.34-1014/f.170907007
[5]	张艾莉,尹梦兰. 人口老龄化对区域技术创新的异质门槛效应研究[J]. 软科学,2019,33(11):35-40. doi: 10.13956/j.ss.1001-8409.2019.11.07
[6]	楼永,王留瑜,郝凤霞. 人口老龄化对我国科技创新的影响分析[J]. 科技管理研究,2020,40(21):14-22. doi: 10.3969/j.issn.1000-7695.2020.21.003
[7]	王艳涛,崔成. 人力资本结构与技术创新模式关系研究[J]. 技术经济与管理研究,2019(6):30-35. doi: 10.3969/j.issn.1004-292X.2019.06.006
[8]	张涵,杨晓昕. 异质性人力资本、空间溢出与高技术产业创新[J]. 科技进步与对策,2019,36(22):51-59. doi: 10.6049/kjjbydc.2019040063
[9]	冯江茹. 人力资本对区域创新效率影响的实证研究[J]. 技术经济,2020,39(12):123-130. doi: 10.3969/j.issn.1002-980X.2020.12.016
[10]	裴开兵. 研发人力资本配置与技术创新−异质教育层次视角[J]. 科技进步与对策,2021,38(14):11-20. doi: 10.6049/kjjbydc.2020100688
[11]	刘灿雷,高超. 教育、人力资本与创新−基于“量”与“质”的双重考察[J]. 财贸经济,2021,42(5):110-126. doi: 10.3969/j.issn.1002-8102.2021.05.008
[12]	卿陶. 人力资本投入与企业创新−来自中国微观企业数据的证据[J]. 人口与经济,2021(3):108-127.
[13]	STEPHAN P E & LEVIN S G. Age and Nobel Prize revisited [J]. Scientometrics, 1993, 28(3):387-399. doi: 10.1007/BF02026517
[14]	NODA H. Population aging and creative destruction [J]. Journal of Economic Research, 2011(16):29-58.
[15]	胡乃军. 中国人口老龄化与居民储蓄研究[J]. 北京科技大学学报(社会科学版),2017,33(2):33-38. doi: 10.3969/j.issn.1008-2689.2017.02.006
[16]	LEE R D. Macroeconomic consequences of population aging in the United States:overview of a national academy report [J]. American Economic Review, 2014, 104(5):234-239. doi: 10.1257/aer.104.5.234
[17]	朱雪忠,胡成. 专利是测度企业技术创新绩效的有效工具吗?[J]. 科学学研究,2021,39(8):1498-1503. doi: 10.3969/j.issn.1003-2053.2021.08.016
[18]	林喜庆,许放. 基于AHP的城市科技人才竞争力评价研究−以中国4个直辖市2008年数据分析为例[J]. 北京科技大学学报(社会科学版),2015,31(1):109-118. doi: 10.3969/j.issn.1008-2689.2015.01.017
[19]	刘智勇,李海峥,胡永远,等. 人力资本结构高级化与经济增长−兼论东中西部地区差距的形成和缩小[J]. 经济研究,2018,53(3):50-63.
[20]	江三良,侯媛媛. 人力资本结构优化与地区经济高质量增长[J]. 南京审计大学学报,2021,18(1):90-100.
[21]	程锐,马莉莉,陈璇. 人力资本结构演进与中国经济增长−来自省际层面的经验证据[J]. 商业研究,2019(1):60-70.
[22]	张红霞,王天慧. 人力资本结构高级化、技术进步与地区经济高质量发展−基于空间杜宾模型的分析[J]. 商业研究,2021(2):30-39.
[23]	蒋长流,司怀涛. 环境规制、研发投入与产业结构调整[J]. 南京财经大学学报,2020(2):18-26.
[24]	温忠麟,叶宝娟. 中介效应分析:方法和模型发展[J]. 心理科学进展,2014,22(5):731-745.
[25]	张晓锋,周昕宇. 高校科研助理岗位系统建构探析[J]. 北京科技大学学报(社会科学版),2021,37(6):630-637. doi: 10.3969/j.issn.1008-2689.2021.06.007